Find Minimum Spanning Tree
Editing Help.FindMinimumSpanningTree
|
Paragraphs: for a new paragraph, use a blank line; |
Line break: \\ or [[<<]] |
|
-> to indent text, -< hanging text |
Join line: \ |
|
Lists: * for bulleted, # for numbered, :term:definition for definition lists | |
|
Emphasis:
''italics''
'''bold'''
'''''bold italics'''''
@@ | |
|
References: [[another page]], [[http://example.com/]], [[another page | link text]], [[#anchor]], [[#anchor | link text]] |
Signatures: name: ~~~ |
|
Groups: [[Group/Page]] displays Page, [[Group.Page]] displays Group.Page, [[Group(.Page)]] displays Group, [[Group/]] links Group homepage |
name and date: ~~~~ |
|
Separators: !!, !!! for headings, ---- for horizontal line |
Prevent formatting: [=...=] |
|
Other:
[+big+]
[++bigger++]
[-small-]
[--smaller--]
'^superscript^'
'_subscript_'
{+inserted+}
{- |
Preformatted: [@...@] or >>pre<<...>><< |
Preview Help.FindMinimumSpanningTree
Page is unsaved
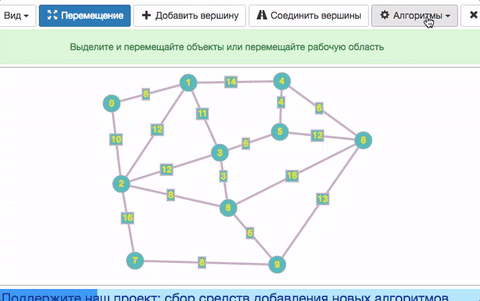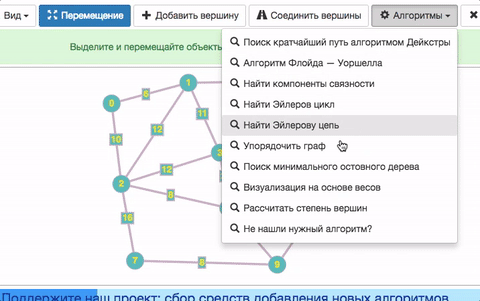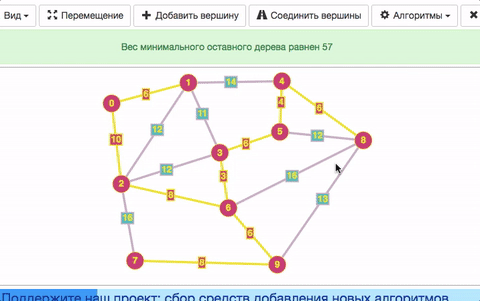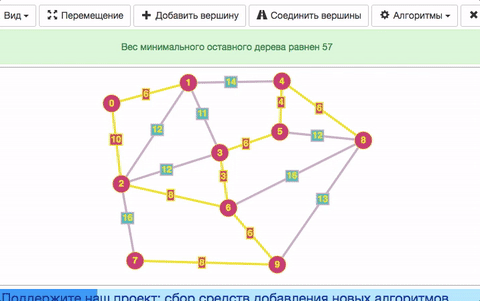
Minimum Spanning Tree
Minimum spanning tree (or minimum weight spanning tree) in a connected weighted undirected graph is a spanning tree of that graph which has a minimum possible weight. The weight of a tree means a sum of the edges’ weights.
In other words, minimum spanning tree is a subgraph which contains all the vertexes of the original graph, while the sum of the arcs’ weights is minimal.
Algorithm usage examples
With the help of the searching algorithm of a minimum spanning tree, one can calculate minimal road construction or network costs.
Searching algorithm
We use Prim’s algorithm for searching.
How to use
- Create a graph.
- Choose “Algorithms” in the menu bar then “Find minimum spanning tree”.
End of preview -- remember to save
Top